1 . 문제 설명
병든 나이트가 N × M 크기 체스판의 가장 왼쪽아래 칸에 위치해 있다.
병든 나이트의 이동 가능한 방향:
- 2칸 위로, 1칸 오른쪽
- 1칸 위로, 2칸 오른쪽
- 1칸 아래로, 2칸 오른쪽
- 2칸 아래로, 1칸 오른쪽
이동 조건:
- 조건 1: 이동 횟수가 4번 초과이면 → 이동 방법을 모두 한 번씩 사용해야 한다.
- 조건 2: 이동 횟수가 4번 이하이면 → 이동 방법에 제한이 없다.
병든 나이트가 방문할 수 있는 칸의 최대 개수를 구한다.
- 체스판의 세로 N, 가로 M: N, M ≤ 2,000,000,000 → long
- 시간 제한: 2초
- 메모리 제한: 128MB
2. 접근 방식
- N과 M의 크기에 따라 경우를 나누어 생각한다.
- N = 1
- 위아래로 움직일 수 없다. 이동 횟수는 0 ⇒ 1칸
- N=2
- 2칸 위아래 이동이 불가능하다. 2번, 3번 이동 방법을 번갈아 사용한다.
- 식으로 나타내면 `(M+1)/2` 이지만, “조건 1”에 따라 최대 이동 횟수가 3번이다.
- M이 8 이상이면 “조건 1”을 만족할 수 없고, 방문할 수 있는 최대 개수가 4로 고정된다.
- ⇒ `min(4, (M+1)/2)`

- M ≥ 7 (= 4가지 이동 방법을 모두 사용 가능한 경우)
- 높이가 3 이상이기 때문에 1번, 4번 이동도 가능하다.
- 4가지 이동 방법을 한 번씩 사용하면 오른쪽으로 6칸 움직이게 된다.
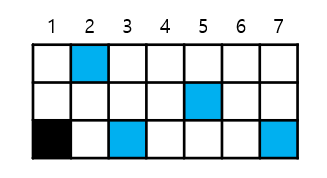
- M=8 부터는 조건1을 만족하기 때문에 최대한 많은 칸을 방문할 수 있는 2번, 3번 이동만 하면 된다.
- 따라서 총 열의 개수 -2 를 해주면 된다.
- ⇒ `M - 2`
3. 최종 코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
long N = Integer.parseInt(st.nextToken()); // 높이
long M = Integer.parseInt(st.nextToken()); // 너비
if (N == 1) System.out.println(1);
else if (N == 2) {
System.out.println(Math.min(4, (M+1)/2));
}
else if (N >= 3) {
if (M < 7) {
System.out.println(Math.min(4, M));
} else { // M >= 7
System.out.println(M - 2);
}
}
}
}시간복잡도: $O(1)$
4. 분석 및 참고사항
입력 크기가 매우 커서 반복문/시뮬레이션 사용이 불가능하다.
조건을 잘 나누어 수학적으로 계산하는 것이 포인트이다. → 수학적 공식 도출 필요
무조건 시뮬레이션으로 접근 말고, 간소화 ( 수학적 풀이) 가 가능한지 먼저 판별 해보기
- N == 1 : 이동 불가 → 방문 1칸
- N == 2 : 세로 이동 제한 → 오른쪽 2칸 이동만 일부 가능
- N ≥ 3 :
- M < 7 : 이동횟수 4번 미만
- M ≥ 7 : 이동방법 모두 사용 가능
https://codeung.tistory.com/203
반응형
'알고리즘 문제 > 백준' 카테고리의 다른 글
| [백준] 4963번: 섬의 개수 (Java) (0) | 2025.08.12 |
|---|---|
| [백준] 18126번: 너구리 구구 - BFS (Java) (3) | 2025.08.11 |
| [백준] 9996번: 한국이 그리울 땐 서버에 접속하지 (Java) (2) | 2025.08.10 |
| [백준] 18126번: 너구리 구구 - DFS (Java) (2) | 2025.08.08 |
| [백준] 2437번: 저울 (Java) (4) | 2025.08.07 |

댓글